Home + About me + E-mail me

Otis King model K Calculator

Extended and ready for action. From the left: the chrome handle (the fixed part); the lower scale (fixed to the handle); the black cursor which slides along and around the fixed part, with two pointers L (left) on the lower scale and T (right) on the upper scales; the upper scales, which slide in and out of the fixed part and can be rotated, they are operated by the knurled knob at the right. In use the handle is usually held by the left hand and the calculator held roughly horizontal and pointing away, looking down onto the scales.

Closed

Multiplication

This is the basic procedure for multiplication, for example 2 times 3. First open the calculator up, if it isn't already, then move the cursor to set its lower pointer L over 2 on the fixed scale at the bottom near the handle:

Then move the top scales to bring the ONE at the centre of the two scales over the upper pointer T on the cursor:

Then move the cursor again to bring the upper pointer T over 3 on one of the upper scales. The right scale is the one that will bring the lower pointer L of the cursor over the lower scale. In this case we move the cursor upwards from the centre ONE:

The result, 6, is then read on the lower scale, under the lower pointer L:

This can carry on indefinitely as the result is in the correct place to start another multiplication. On the model K (like this one), which has two conventional logarithmic scales at the top, it is always possible for the second move to set the centre ONE under T. On the model L, which has only one normal upper scale, it is necessary at times to use the ONE at the top instead. The model L has a scale for reading logarithms as the lower of the two upper scales; this makes it more powerful but less easy to use for simple calculations.

Division

Division can be shown from the same images in a different order. To divide 6 by 3 first set 6 under the lower cursor L:

Then move the upper scale to bring 3 under the pointer T:

Then move the cursor pointer T to the ONE index in the centre of the two upper scales:

And finally read the answer 2 under the lower pointer L:

Again the result is under L on the lower scale, so multiplication and division can be chained in any order.

In some cases in may be necessary to use a different ONE on the upper scale to get in range with the lower scale.

(You can see from the last image that the scales are printed on paper then wrapped around the cylinder; the oblique evening sun under which this photo was taken has pulled a shadow from the slightly raised edge where the glue is failing.)

How it works

Operation is very similar to a conventional slide rule, which is described here.

The diagrams show how the cursor is used to add distances from the two separated scales. To make this clear, the scales are shown as simple linear scales rather than spirals. The left-hand scale is the lower, fixed scale near the handle, the right-hand scale the upper, moveable scale and the block at the bottom is the cursor with its two marks. The cursor is shown rather longer than the real one, as my scales don't fit one down inside the other like on the real instrument.

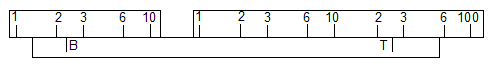
The first move is to put the cursor pointer B over 2 on the lower scale. Cursor B is then at a distance representing log(2) from the index mark of this scale.

Then the upper scale is moved to bring an index mark under the upper cursor mark T.

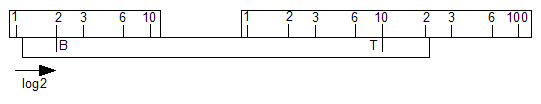
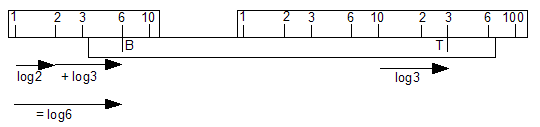
The cursor is then moved to bring cursor mark T over the 3 on the upper scale. This moves the cursor by a distance representing log(3). As the pointers are at a fixed separation, the lower cursor marker B also moves by log(3), and as it started at log(2) it now represents log(2) + log(3) which is log(6). So the result is found under B.

The critical distance for accuracy is the distance along the spiral scale. This is stored as rotation of the cursor or scale, with the axial movements counting the number of complete turns. So when placing the cursor marks the angular position must be precise if accuracy is not to be lost, but axial position error is insignificant unless it is so large that the result is read from the wrong turn, an error of twentieth-root of ten. The instrument would (in theory) work just as well if each cursor point had a peg that fitted into a groove that ran along the spiral track. Then it would be more clear that these are folded 1-dimensional movements rather than the apparent two-dimensional movements; of course it were like this it would be tedious to use as you'd have to turn the cursor and end scale dozens of times in the course of a calculation.

My slide rules + How to use a slide rule + Note on accuracy

Home + About me + E-mail me

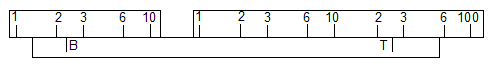
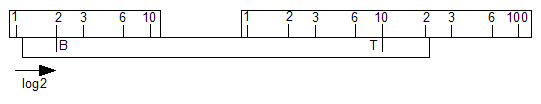
2008-04-17 .. 2008-05-25 (+44 7010 700642)