

The theory of operation of the Fuller is similar to a conventional slide rule (for which see here) but the moves are different in practice. The Fuller has only one logarithmic scale so you cannot add the distances by sliding one scale against another. Instead you use a pair of linked pointers to store a distance read from the scale, representing one argument, and then use the scale again to add the second argument, and the scale again to read off the result.
The diagrams below show the principle, but using a single 1-dimensional scale, rather like using a conventional slide rule with the slide missing and a pair of dividers to carry distances.
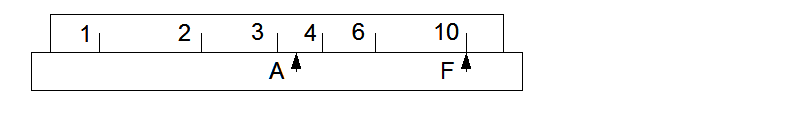
The lower part is the base or fixed part. It carries a fixed pointer F and a second pointer A which can be moved relative to the base. The top part, the scale, also moves relative to the base, independent of A.
To multiply 2 by 3, first move the scale so that 2 is over the fixed pointer.
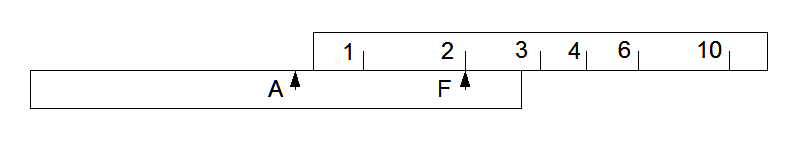
Then move pointer A until it aligns with the index on the scale. The distance from A to F now represents the scale length (logarithm) for 2.
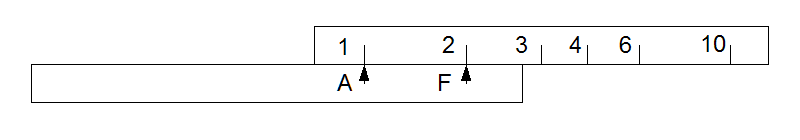
Next move the scale again to bring the second argument 3 against pointer A. Then the scale length for 3 is added to the scale length for 2, stored as the distance A to F, and the answer 6 can be read off the scale opposite pointer F.

On the real calculator the scale is actually a helix wrapped 50 times around a cylinder. Pointer A and the scale can both be moved in 2 directions relative to the base part, angularly and axially. Pointers A and F effectively store the distance along the scale as an angle plus the number of turns. The base is the middle cylinder of the calculator, the scale cylinder moves outside the base and the cylinder carrying the pointer A moves inside the base cylinder. Pointer A has two locations exactly one scale length apart, whichever is more convenient is used.
The scale has written marks for every 3-digit value and tick marks for the fourth digit or every other fourth digit depending on position along the scale. The accuracy does not scale up quite as far as you would expect for the long scale as the pointers are quite a bit more wobbly and vague than the slide and cursor on a small linear slide rule, but it gives 4 significant figures easily.
To divide 6 by 3, first move the scale to set 6 under F.
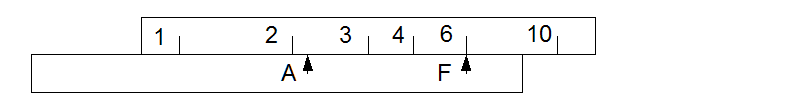
Then move pointer A to align with 3.

Then move the slide again to bring the index mark to align with A and read the result 2 under F.
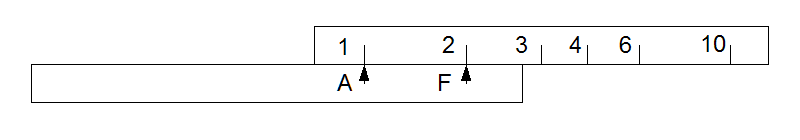
Note that both multiplication and division leave the result under the F pointer, and that they start with the multiplicand or dividend under F, so chaining in any sequence is simple.

This picture, of the calculator opened out, shows the parts. Part 1 is the base part, which carries the fixed pointer F. Part 2 slides within the base and carries the moveable pointers A. Part 3 is the sliding scale and it moves outside the base part.
Now let us repeat the multiplication above on the real machine. First move the scale to put 2 on the scale under pointer F.

Then bring the pointer A up to the index mark on the scale. The index is the 100 at the top.

Then move the scale again to align 3 with the A pointer. Look under pointer F for the result, 6.

The last picture shows a general view of the calculator at the end of this process.

My slide rules + How to use a slide rule + Note on accuracy
 2008-04-12 .. 2008-04-13
(+44 7010 700642)
2008-04-12 .. 2008-04-13
(+44 7010 700642)