

This a neat pocket-watch-like mechanical slide rule calculator, with an effective scale length of about 750mm.
The theory of operation of the Fowler is similar to a conventional slide rule (for which see here) but the moves are different in practice. The Fowler has only one logarithmic scale so you cannot add the distances by sliding one scale against another. Instead you use a pair of pointers to store a distance read from the scale, representing one argument, and then use the scale again to add the second argument, and the scale again to read off the result.
The diagrams below show the principle, but using a 1-dimensional linear scale, rather like using a conventional slide rule with the slide missing and a pair of dividers to carry distances.
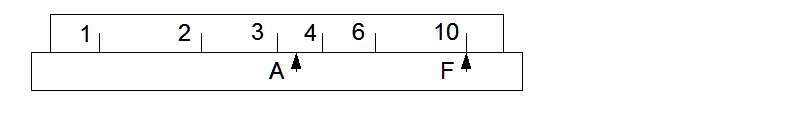
The lower part is the base or fixed part. It carries a fixed pointer F and a second pointer A which can be moved relative to the base. The top part, the scale, also moves relative to the base, independent of A.
To multiply 2 by 3, first move the scale so that 2 is over the fixed pointer.
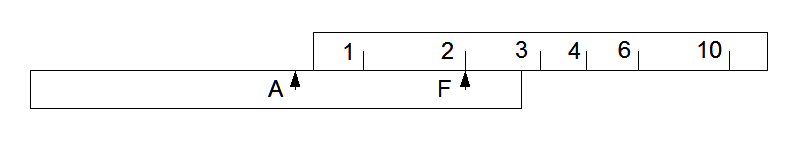
Then move pointer A until it aligns with the index on the scale. The distance from A to F now represents the scale length (logarithm) for 2.
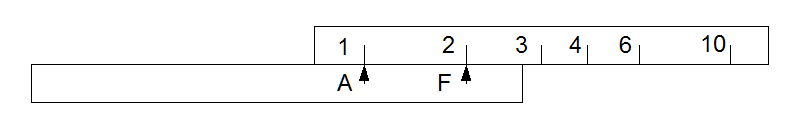
Next move the scale again to bring the second argument 3 against pointer A. Then the scale length for 3 is added to the scale length for 2, stored as the distance A to F, and the answer 6 can be read off the scale opposite pointer F.

On the real calculator the scale is actually a circle or a group of circles. Pointer A and the scale can both be rotated relative to the base part. Between them pointers A and F store a distance along the scale.
To divide 6 by 3, first move the scale to set 6 under F.
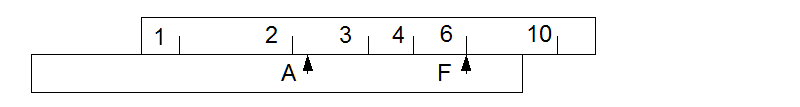
Then move pointer A to align with 3.

Then move the slide again to bring the index mark to align with A and read the result 2 under F.
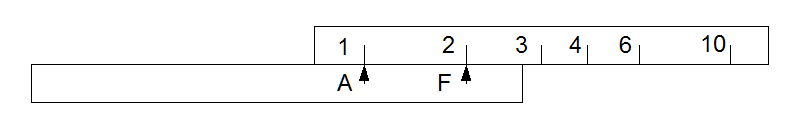
Note that both multiplication and division leave the result under the F pointer, and that they start with the multiplicand or dividend under F, so chaining in any sequence is simple.
Now let's look at the real calculator, for example we'll try to multiply 2 by 3, initially using the short scale. First turn the top knob to align 2 on the outer scale with the fixed pointer F at the top.
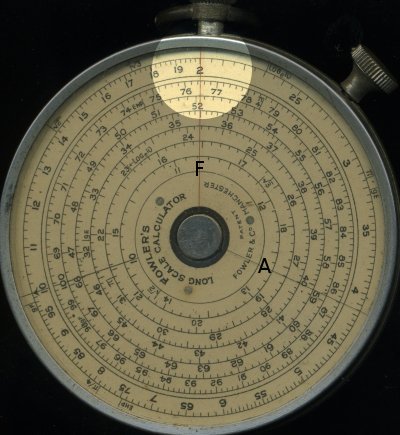
Then use the side knob to bring the moving pointer A up to the index or "10" mark on the scale.

Finally turn the top knob again to bring 3 on the outer scale under the moving pointer A. The result, 6, can be read on the outer scale under the fixed pointer F at the top.

We can then repeat the operation using the long scale. The operations are just the same except we have to choose which of the six turns of the long scale we have to use. First bring up the 2 under the fixed pointer. 2, for which we use the mark labelled "20" (remembering that slide rules do not give powers of ten, you have to work them out for yourself), is found on the second circle out from the centre.

Then as before move the pointer A to the index of the scales. This is always the same place, for both the short and long scales.

Lastly bring the "30" mark under the pointer A. The "30" mark is on the third scale out from the centre. The result is then any of the numbers on the six long scales under fixed pointer F: about 13, 19, 28, 41, 60 or 88.
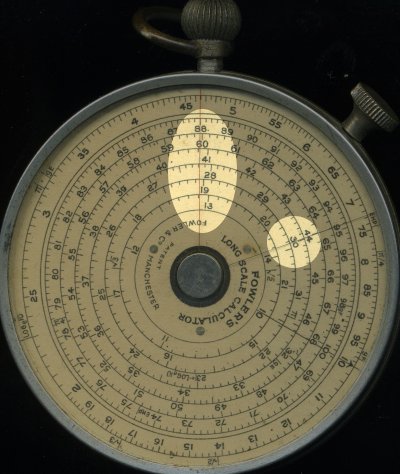
From the short scale calculation we know the result is about 60, so we read the result, which we know is 6, from the 5th scale.
Although it is tedious to have to calculate everything twice, it is good practice as it is easy to make mistakes on this sort of mechanical calculator, and the self-checking from doing the same calculation in slightly different ways is useful.
One point I don't understand is why the long scale is provided as six separate concentric circles rather than a 6-turn spiral. There seems no good reason to do this, unless it was to get round a patent, and it makes reading and setting awkward near a value where the jump occurs from one scale to the next. In the picture below, coming towards the end of the first circle is the numbered mark for 1.4, followed by tick marks for 1.41 to 1.46. The tick marks for 1.47 to 1.49 and the numbered mark for 1.5 are on the second scale. The transition point is actually 1.468, the sixth-root of 10. Not only is this confusing to read, but interpolating between 1.46 and 1.47 is difficult.

It's fairly easy to interpolate the scales to three figures, with a partial fourth figure in the lower half of the scale. The mechanical accuaracy is good and the cursor lines and scale markings are narrow and easy to align. It should be possible to achieve around 0.2% per calculation, based on 0.5mm total error for the four steps.
My slide rules + How to use a slide rule + Note on accuracy
 2008-04-17 .. 2008-04-19
(+44 7010 700642)
2008-04-17 .. 2008-04-19
(+44 7010 700642)